2021. 6. 15. 17:06ㆍ컴퓨터 공학/알고리즘
📕그래프는 뭘까?
알고리즘에서의 그래프는 '간선들로 연결된 정점들의 집합'이라고 얘기할 수 있다.
그럼 정점은 뭐고 간선은 뭐냐?

정점(vertex)은 흔히 노드(node)라고 알려져 있는 점이다.
그리고 이 점과 점을 연결한 선이 바로 간선(edge)이다.
그리고 이 간선은 방향이 있을 수도 있고, 없을 수도 있다.
방향이 있는 그래프를 directed graph(방향 그래프)라고 하고
방향이 없는 그래프를 undirected graph(무방향 그래프)라고 한다.
그래프에는 '사이클'이라는 개념이 있다.
말 그대로 사이클, 즉 자기 자신으로 돌아오는 길이 있는 것을 사이클이라고 한다.
하지만 트리는 이 '사이클'이 존재하지 않는다.
정확히는 사이클이 존재하지 않는 그래프를 트리라고 한다.
📕그래프를 나타내는 방법
그래프를 나타내는 방법은 세 가지가 존재한다.
하나는 간선들의 집합으로 표현하는 방법,
또 다른 방법은 인접 행렬로 표현하는 방법이고,
인접 리스트로 표현하는 방법이다.
이 문서에서는 주로 인접리스트로 그래프와 트리를 다룰 것이다.


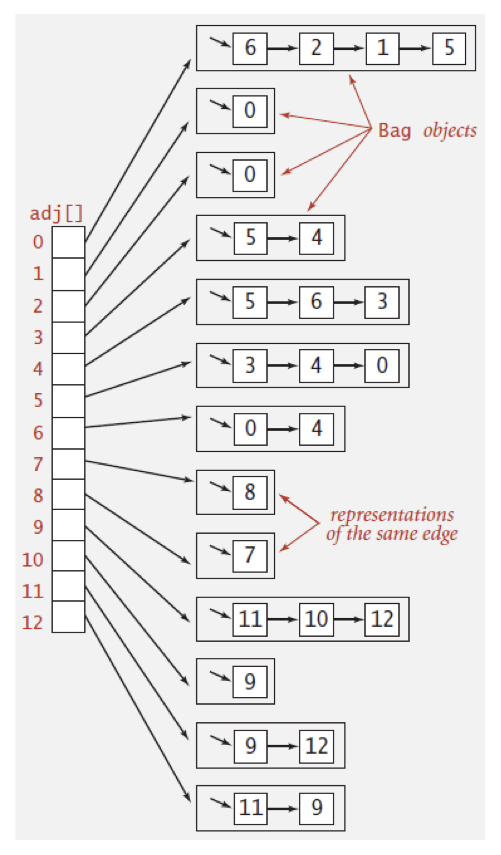
📕그래프 탐색 (DFS, BFS)
탐색의 목적이 무엇인가?
바로 어떠한 값 혹은 비용을 찾기 위함이 아닌가!
그래프 탐색도 마찬가지이다. 그리고 이 그래프 탐색은 같은 곳을 두 번 탐색하지 않기 때문에,
시간 복잡도 O(V+ E)로 가능하다. (vertex & edge)
그래프 탐색은 보통 소스 노드 S로부터 모든 노드를 방문하는 방식으로 탐색한다.
방문하지 않은 노드를 방문하고, 방문처리를 하며 모든 노드를 방문했을 경우 작업을 종료한다.
그렇다면 먼저 BFS에 대해서 알아보자.
BFS는 Breadth-First Search의 준말로 우리말로 '너비 우선 탐색'이라고 불린다.
주로 최단경로를 찾는 알고리즘에 사용되며, 무방향 그래프의 비용을 계산할 때 사용된다.
'큐' 자료구조를 이용하며, 시간 복잡도는 O(V+E)이다.
인접 리스트인 다음과 같은 리스트가 있다.
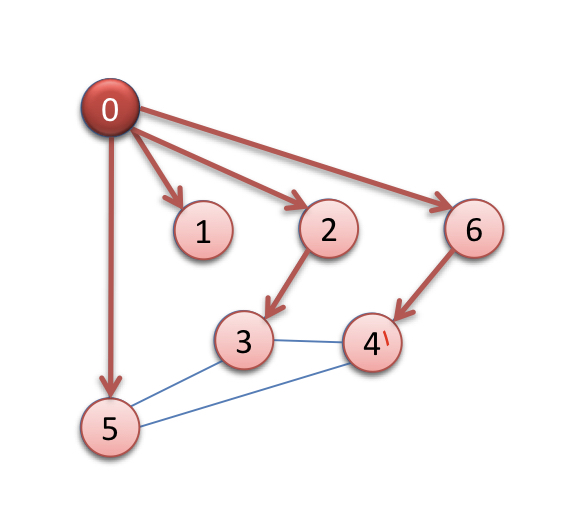
0 6 2 1 5
1 0
2 0
3 4 5
4 5 6
5 4 3 0
6 0 4
노드 0은 노드 6, 2, 1 ,5와 연결되어 있고
노드 3은 노드 4, 5와 연결되었고...
이런 식으로 각각의 노드가 연결되어 있다.
그렇다면 이 그래프는 어떻게 BFS로 탐색할까?
아래의 의사 코드를 보자.
BFS(graph G, start vertex s)
mark s as explored
let Q = queue
add s to Q
while Q != empty:
v = Q.dequeue()
for each edge(v.w):
if w unexplored
mark w as explored
add w to Q
먼저 시작 노드 0을 방문 처리하고 큐에 넣음으로써 탐색을 시작한다.(모든 순서는 방문, 큐 삽입 순서이다.)
이후 큐에 있는 0을 꺼냄으로써 0과 인접해 있는 6, 2, 1, 5 노드를 확인하고, 노드들을 방문 처리하고 큐에 삽입한다.
그럼 이때 큐의 front() 노드는 무엇인가? 바로 6이다
그럼 6을 큐에서 꺼내고, 6과 인접해 있는 노드 4, 0 노드를 확인하고, 4를 방문 처리하고 큐에 삽입한다.
0을 방문처리를 해야 하는데 여기서 문제가 있다.
바로 0은 이미 방문을 했다는 것이다.
그렇기 때문에 0은 다시 방문처리를 하지 않고, 방문처리를 하지 않았기 때문에 큐에 넣지 않는다.
그럼 현재 큐에 있는 값은 무엇인가?
현재 2, 1, 5, 4 순서로 큐에 있는 것이다.
이런 식으로 반복하면 노드 탐색 순서는
6->2->1->5->4->3이 될 것이다.
(코드는 후에 기술하겠다.)
BFS가 최단 경로를 찾을 때 사용된다고 말했는데, 그 이유는 거리에 따라서 탐색 비용을 1씩 추가해서 계산하기 때문이다.
즉 위의 그래프에서는 6,2,1,5를 탐색하는 비용은 1이고,
3, 4를 탐색하는 비용은 2이다.
DFS에 대해서 알아보자.
DFS는 Depth First Search의 약자로 '깊이 우선 탐색'이라고 한다.
DFS는 주로 길이 있는지 탐색하는 Path finding에서 사용된다.
BFS와 반대로 '스택'자료구조를 사용하고, 시간 복잡도는 마찬가지로 O(E + V)이다.

0 6 2 1 5
1 0
2 0
3 4 5
4 5 6
5 4 3 0
6 0 4
DFS는 스택 자료구조를 사용하기 때문에 탐색 순서가 BFS와는 다르다.(스택은 LIFO, 큐는 FIFO)
탐색과정을 의사 코드로 구현하면 다음과 같다.
DFS(graph G, start vertex s)
let ST = stack
add s to ST
while St != empty:
v=ST.pop();
mark v as explored
for each edge(v, w):
if w unexplored
add w to ST
DFS 역시 거리가 짧은 순으로 방문한다.
먼저 6을 방문하고, 6과 인접해 있는 노드 중 가장 가까운 0을 방문해야 하지만
0은 이미 방문처리가 되어 있기 때문에 4를 방문한다.
4를 방문하고 4와 가장 가까운 5를 방문하고
5와 가장 가까운 4를 방문해야 하지만 4가 이미 방문처리되어 있기 때문에 3을 방문한다.
3을 방문하면 인접 노드인 4, 5가 모두 방문처리되어 있기 때문에 이전 단계로 돌아간다.
이전 노드인 5의 인접 노드도 모두 방문처리되어 있기 때문에 이전 단계로
이전 노드인 4도, 6도 모두 인접 노드가 방문 처리되어 있기 때문에 0으로 돌아가게 되고
0에서 방문처리되지 않은 가장 가까운 노드인 2를 방문하고 다시 1을 방문함으로써
탐색은 끝나게 된다.
노드를 탐색하는 순서는 6->4->5->3->2->1 순이다.
📕트리 및 최소 신장 트리(MST)
앞에서 잠깐 언급을 했지만
트리는 그래프의 범주에 들어가며, 사이클이 없이 연결되어 있는 무방향 그래프를 말한다.
그렇다면 spanning tree는 뭘까?
스패닝 트리, 신장 트리는 그래프 G에 모든 노드들이 포함되어 있는 트리를 말한다.
다시 말해서 어떤 경로로든 모든 노드에 방문할 수 만 있으면 된다.
그렇다면 최소 신장 트리, minimum spanning tree는 뭘까?
신장 트리를 구성하는 비용이 가장 적은 트리가 바로 최소 신장 트리가 되는 것이다.
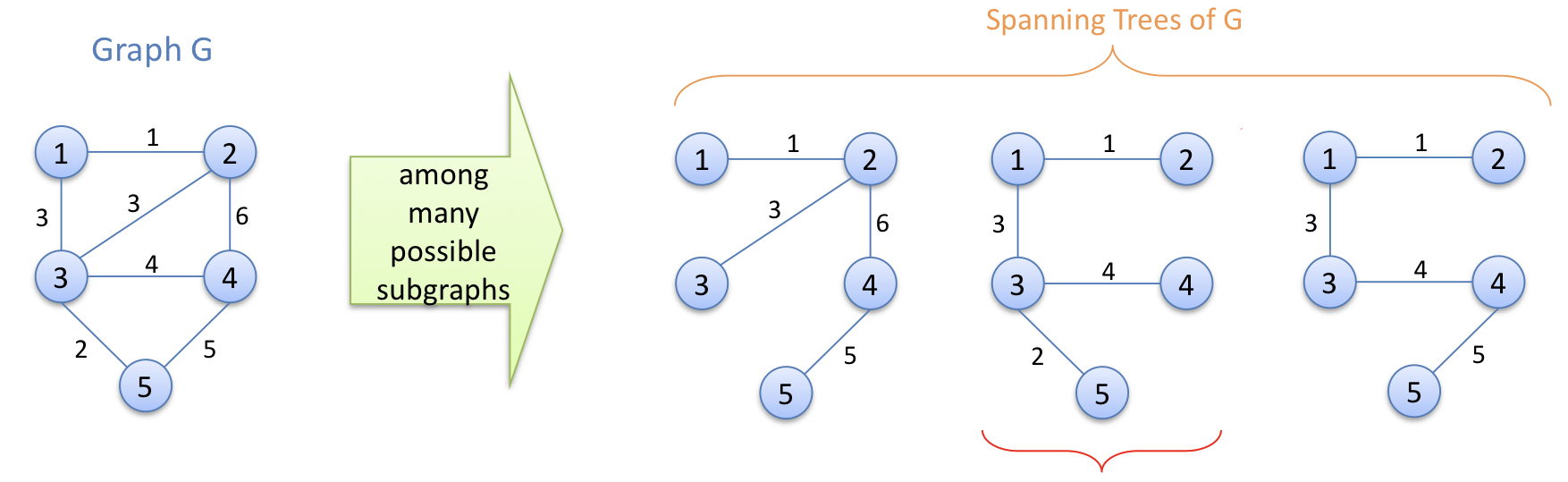
위의 사진에서 볼 수 있듯, 두 번째 트리가 바로 최소 신장 트리, MST가 된다.
그렇다면 우리는 어떻게 최소 신장 트리를 찾을 수 있을까?
트리에 비용이 있는 간선이 존재하고, 트리가 연결되어 있으면 MST는 유니크(unique)하다!
그리고 우리는 이 탐색과정을 그리디한 접근법으로 탐색이 가능하다.
📕Kruskal's algorithm(크루스칼 알고리즘)
그리디 한 접근법으로 최소 신장 트리를 만드는 방법 중 하나가 바로 크루스 칼 알고리즘이다.
크루스 칼의 알고리즘은 safe edge를 찾는 탐색 방법으로, v와 e를 연결하는 최소 간선을 찾아 연결하는 알고리즘이다.
최소 간선을 연결한다고 했는데, 그럼 순서대로 다 연결하면 되는 것 아닌가?!라고 생각할 수 있지만
여기에 조건이 붙는다. 바로 사이클을 생성하지 않을때 까지! 그리고 간선이 V-1개가 될 때까지!

위의 트리를 보자.
노드가 0번부터 7번까지 총 8개의 노드가 존재한다.
그리고 각 노드로부터 다른 노드로의 비용은 오른쪽에 오름차순으로 정렬되어 있다.
노드 0을 시작으로 0-7이 최소비용이기 때문에 7을 트리 T와 연결하여 같은 집합으로 만든다.
그다음 최소 비용인 2-3 간선을 연결하고, 5-7 간선까지 연결한다.
그리고 1-3 간선을 연결하려는 순간! 사이클이 형성된다.
1-3 간선이 연결되면 0에서 7, 1, 3, 2를 거쳐 0으로 다시 돌아올 수 있는 사이클이 형성되기 때문에
1-3 간선은 추가하기 않느다.
위의 알고리즘대로 간선을 추가하면 왼쪽 사진과 같은 최소 신장 트리가 만들어진다.
그럼 여기에서 의문이 든다. 어떻게 사이클을 형성하는지 알 수 있을까?
이때 우리는 union-find 혹은 disjoint-set 자료구조를 사용하는데, 이는 추가로 문서를 작성하도록 하겠다.
크루스 칼 알고리즘의 시간복잡도는 O(E logE)이다.
📕Prim's algorithm(프림 알고리즘)
프림 알고리즘 역시 크루스 칼 알고리즘처럼 그리디한 알고리즘이다.
다만 크루스칼 알고리즘은 최소비용인 트리를 순서대로 트리 집합에 추가했다면
프림 알고리즘은 지금까지 추가한 트리 집합과 가장 최소비용인 노드를 추가한다.
프림 알고리즘도 간선의 개수가 V-1개가 되면 작업을 종료한다.
- Start with vertex 0 and greedilty grow T
- Add to T the min weight edge with exactly one edpoint in T
- Repeat until V-1 edges

프림 알고리즘을 구현하는 방법에는 여러 가지 방법이 있는데
우리는 PQ 즉, 바이너리 힙으로 구현할 것이며, 바이너리 힙으로 구현하는 방법에도 두 가지 방법이 있다.
하나는 Lazy 한 방법, 또 다른 하나는 Eagle한 방버이 있다.
Lazy한 프림 알고리즘은 edge를 PQ의 key로 사용하고, 간선의 비용을 min_heap으로 정렬하는 방식이다.
Eagle 한 프림알고리즘은 vertex를 PQ의 key로 사용하고,
트리 T와 가장 가까운 노드를 우선순위로 정렬한다.
즉, 최소비용 간선으로 연결된 정점을 선택하여 신장 트리 집합에 추가하는 방식이다.
이 글에서는 Eagle한 방법을 알아보겠다.


트리 T의 정점 0으로부터 시작한다.
0에서 가장 적은 비용의 노드 7을 우선적으로 트리 T에 추가한다.
그리고 트리 T에서 갈 수 있는 1, 5, 4, 2, 6의 노드 중에서 가장 저렴한 비용으로 갈 수 있는 노드인
1을 트리에 추가한다.
다시 T에서 최소비용으로 갈 수 있는 노드 2를 T에 추가한다.
위의 방식을 노드가 V-1개가 만들어질 때까지 반복하면 최소 신장 트리를 얻을 수 있다.
아래 의사 코드르 보자.
MST-Prime(G, w, r)
for each u ∊ G.V
u.key = INF
u.𝜋 = NIL
r.key = 0
PQ = G.V
while PQ != 0
u = Extract_min(PQ)
for each v ∊ G.Adj[u]
if v ∊ Q and W(u,v) < v.key
v.𝜋 = u
v.key = w(u,v)
Lazy 한 프림 알고리즘의 시간 복잡도는 O(E log E)이고
Eager 한 프림 알고리즘의 경우 바이너리 힙으로 구현한 경우 O(E logV), 피보나치 힙으로 구현한 경우 O(E+ VlogV)이다.
'컴퓨터 공학 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 선택정렬, 삽입정렬 구현(C/C++) (0) | 2021.07.23 |
|---|---|
| [알고리즘] 다익스트라, 벨만포드 알고리즘(Dijkstra & Bellman-ford) (0) | 2021.06.18 |
| [알고리즘] 기수정렬/ radix sort (0) | 2021.06.15 |
| [알고리즘] Backtracking / 백트래킹 (0) | 2021.06.13 |
| [알고리즘] Huffman code / 허프만코드 (0) | 2021.06.13 |